Wprowadzenie
Odchylenie standardowe (pierwiastek z wariancji) w kilku słowach informuje, ile średnio wartości odchylają się +/– od średniej arytmetycznej [1].
Odchylenie standardowe oblicza się jako pierwiastek kwadratowy z wariancji. Zatem wyznaczenie wariancji można traktować jako etap pośredni do obliczenia odchylenia standardowego.
Prosto rzecz ujmując informuje ono, jak szeroko wartości jakiejś zmiennej np. wiek, kurs akcji itp. są rozrzucone wokół średniej.
W zarządzaniu ryzykiem (finansach, tradingu) odchylenie standardowe często wykorzystuje się jako miarę zmienności danego instrumentu finansowego, zaś średnią arytmetyczną jako oczekiwaną stopę zysku.
Wyróżnia się [2]:
- odchylenie standardowe zmiennej losowej, będące właściwością badanego zjawiska. Daje się ono obliczyć na podstawie ścisłych informacji o rozkładzie zmiennej losowej. Rozkład ten w praktycznych badaniach nie jest zwykle znany.
- odchylenie standardowe w populacji, które jest liczbą dającą się obliczyć dokładnie, jeśli znane byłyby wartości zmiennej dla wszystkich obiektów populacji; odpowiada odchyleniu zmiennej losowej, której rozkład jest identyczny z rozkładem w populacji.
- odchylenie standardowe z próby, które jest oszacowaniem odchylenia standardowego w populacji na podstawie znajomości wyłącznie części jej obiektów, czyli właśnie tzw. próby losowej. Stosowane do tego celu wzory nazywane są estymatorami odchylenia standardowego.
Ja obliczyć odchylenie standardowe w Excelu?
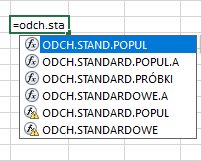
W programie Excel 2016 dostępne są następujące funkcje pozwalające na obliczenie odchylenia standardowego[3]:
ODCH.STAND.POPUL(liczba1;[liczba2];…)
Funkcja ODCH.STAND.POPUL zakłada, że jej argumenty to cała populacja. Jeśli dane reprezentują próbkę populacji, odchylenie standardowe należy obliczyć za pomocą funkcji:
ODCH.STANDARDOWE.PRÓBKI(liczba1;[liczba2];…)
Powyższe funkcje pomijają wartości logiczne i tekstowe. W przypadku gdy jest konieczność uwzględnienia takich wartości istnieje możliwość wykorzystania poniższych funkcji:
ODCH.STAND.POPUL.A(wartość1;[wartość2];…)
ODCH.STANDARDOWE.A(wartość1;[wartość2];…)
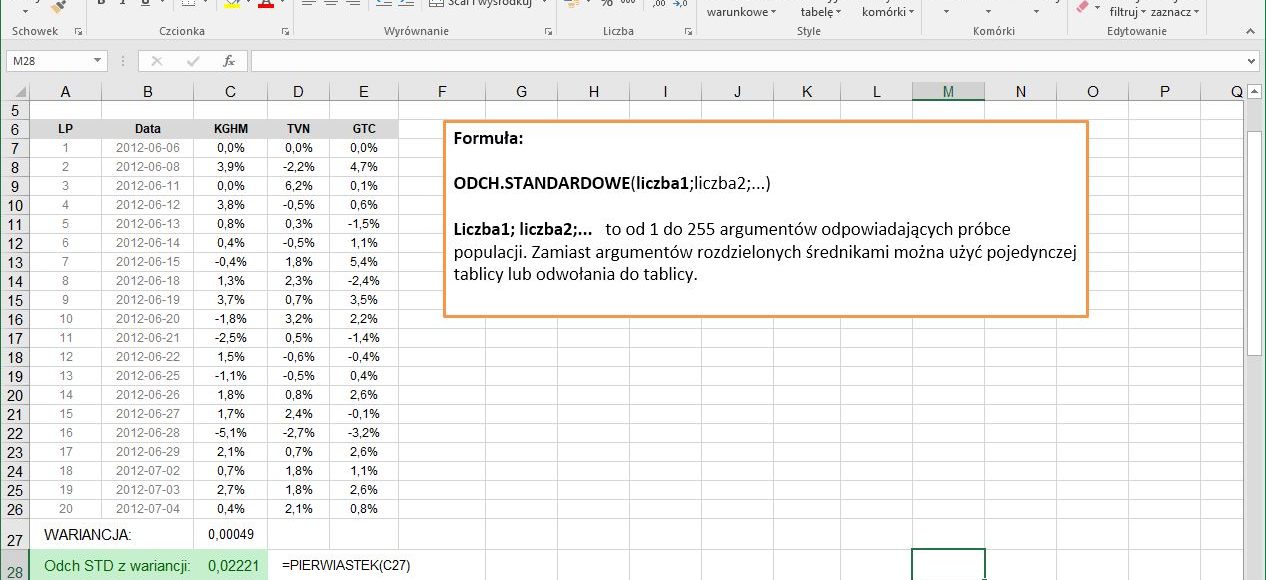
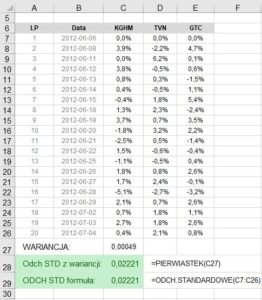
Wykorzystując obliczenia z przykładu dotyczącego kalkulacji wariancji, poniżej screen pokazujący wykorzystanie funkcji obliczającej odchylenie standardowe. Przykładowy plik jest do pobrania poniżej tekstu.
Odchylenie standardowe stóp zwrotu – kalkulator
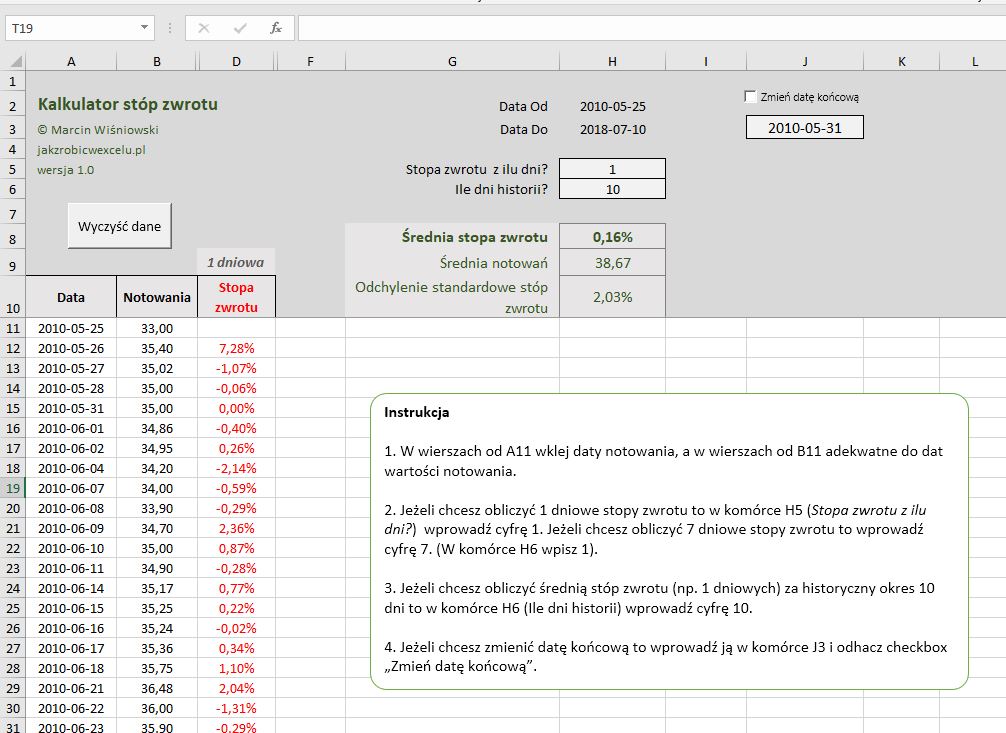 Jeżeli jesteś zainteresowany, to zapraszam do zapoznania się z przygotowanym przeze mnie kalkulatorem, który pozwala na uniwersalne obliczenia:
Jeżeli jesteś zainteresowany, to zapraszam do zapoznania się z przygotowanym przeze mnie kalkulatorem, który pozwala na uniwersalne obliczenia:
- stóp zwrotu w zakresie od 1 do n-dniowej,
- średniej za okres historyczny obliczonych n-dniowych stóp zwrotu,
- odchylenia standardowego obliczonych stóp zwrotu.
Kalkulator pozwala także ograniczyć historię obliczeń przez zmianę daty końcowej serii danych.
[1] źródło: P. Tatarzycki: „Statystyka po ludzku”, Wydawnictwo Złote Myśli, 2008r., str. 160
[2] źródło: https://pl.wikipedia.org/wiki/Odchylenie_standardowe
[3] źródło: https://support.office.com/pl-pl/Search/results?query=ochylenie+standardowe